こんにちは。
本日のブログ担当でございます。
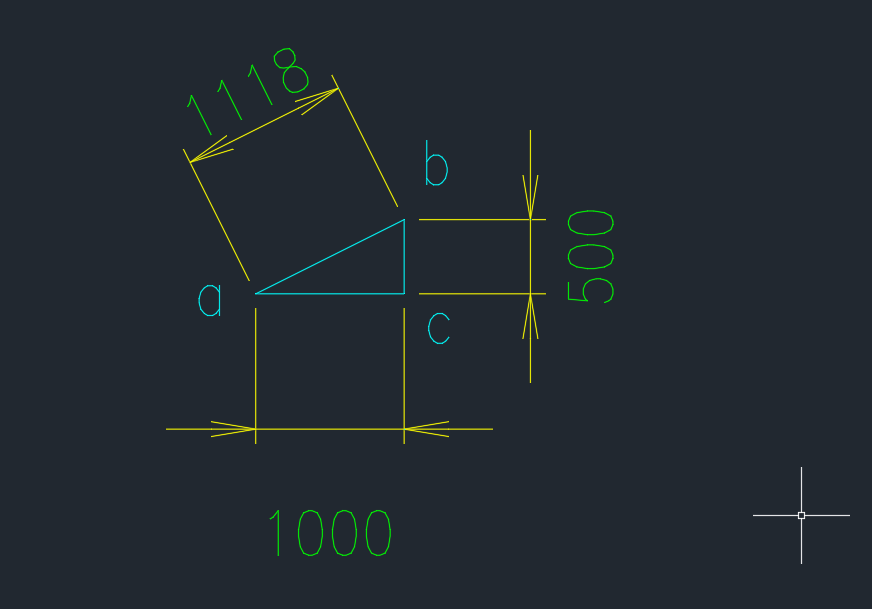
上記画像のようなa地点からb地点へ直接走る場合とc地点を経由する(実際の道を歩くとこんな感じかもしれません)場合では、どれだけ差がでるか計算してみました。
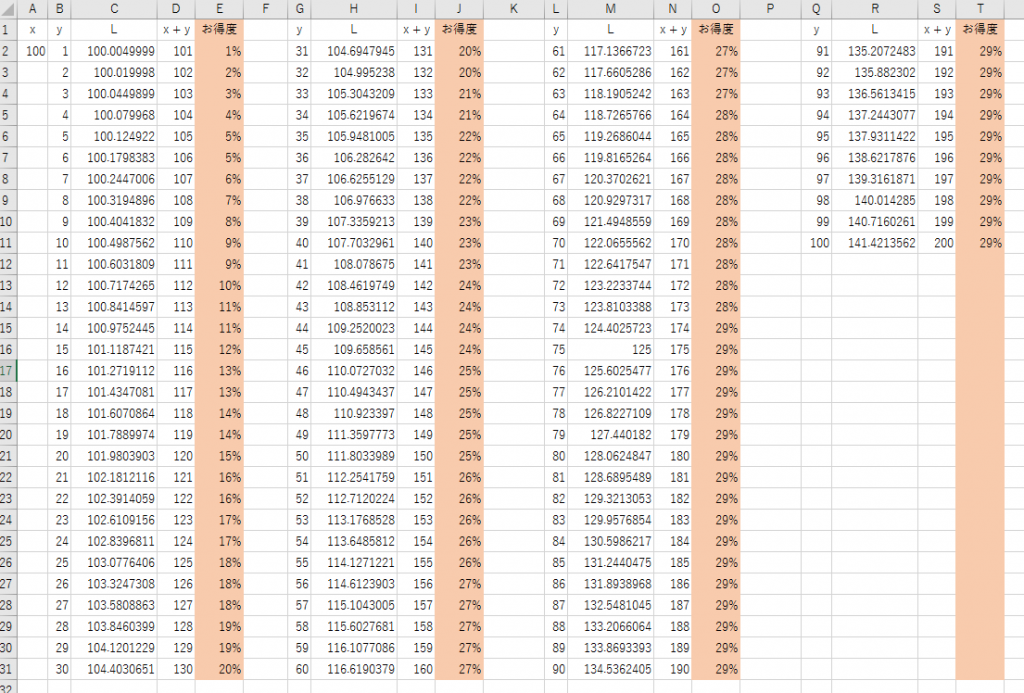
x, y, L はそれぞれ2点ac, bc, ab 間の距離です。
Lは =SQRT(A$2^2 + B2^2) で(三平方の定理で)出しています。
お得度の定義は、(x + y – L) / (x + y) です。yの値が増えるにつれて、お得度が上がっていきます。
斜めに走ったとき、直角に走ったときに比べて何%距離が短くなっているかを表しています。
こちらの値は、∠bacをθとして、(Lsinθ + Lcosθ – L) / (Lsinθ + Lcosθ) となってLは全て消してもいいことが分かります。つまりsinとかcosで表されている関数だということです。
斜めに走ったらどれだけお得か、を知りたくなったら三角関数に頼るか実際に走ってみるかのどちらかですね。